The Beauty of Bézier Curves

The Ever so Lovely Bézier Curve

What is a Bezier curve?

A Bézier curve (/ˈbɛz.i.eɪ/ BEH-zee-ay) is a parametric curve used in computer graphics and related fields.

A set of discrete "control points" defines a smooth, continuous curve by means of a formula.

Usually, the curve is intended to approximate a real-world shape that otherwise has no mathematical representation or whose representation is unknown or too complicated.

The Bézier curve is named after French engineer Pierre Bézier (1910–1999), who used it in the 1960s for designing curves for the bodywork of Renault cars. Other uses include the design of computer fonts and animation.

Bézier curves can be combined to form a Bézier spline, or generalized to higher dimensions to form Bézier surfaces. The Bézier triangle is a special case of the latter.

一条贝塞尔曲线是由一组 Points 从 P0 ～ PN 所控制的，这边 N 就是他的顺序（比如 N=1 的时候是线性的，2 的时候是二次，等等）。第一个控制点和最后一个控制点是曲线的终点；然而中间的一些控制点（如果有），通常不在曲线上。这些点的组合可以理解为仿射组合（affine combination，也就是不仅有点，还有点指向的方向），他们的系数之和等于一。

贝塞尔曲线是由一堆点的集合绘制而成。
这一堆点是在定义的 P0 ～ PN 的控制之下得出的。
P0 ～ PN 这些定义的点，第一个点和最后一个点是曲线的开头和结尾。

One Times Bézier curves

线性 Bézier curves 是由两个点 P0 和 P1 控制形成的，假设我们有两个点 P0 and P1 分段连接，想象第三个点在这两点之间 P,第三个点 P 定义一个 t 值这个 t 的 value 就是介于 0 - 1 之间的值作为百分比

当 t 等于 1 时说明 P 移动到了 P1
当 t 等于 0 时说明 P 移动到了 P0
在中间 t 的值是 0 - 1 之间的值
这个函数也叫做线性插值 lerp

在数学中你可以把它定义为

P = lerp(P0, P1, t)
P = (1-t)P0 + tP1

function lerp (P0, P1, T) {
  return (1 - T)P0 + TP1
}

P = lerp(P0, P1, t)
P = (1-t)P0 + tP1

function lerp (P0, P1, T) {
  return (1 - T)P0 + TP1
}

Two Times Bézier curves

如果我们添加一个新的点, 把两条线段的 P 点连接起来, 我们在继续从这条线段增加一个 P 点, t 的 value 也可以发生变化,这样就形成了二次贝塞尔

继续添加一个点形成三条线段三条线段又有各自的 t 点, 连接他们在连接上的两条线段增加两个点, 这时候我们形成了两个插值点, 从中间再添加一个插值点这样就会形成一个曲线

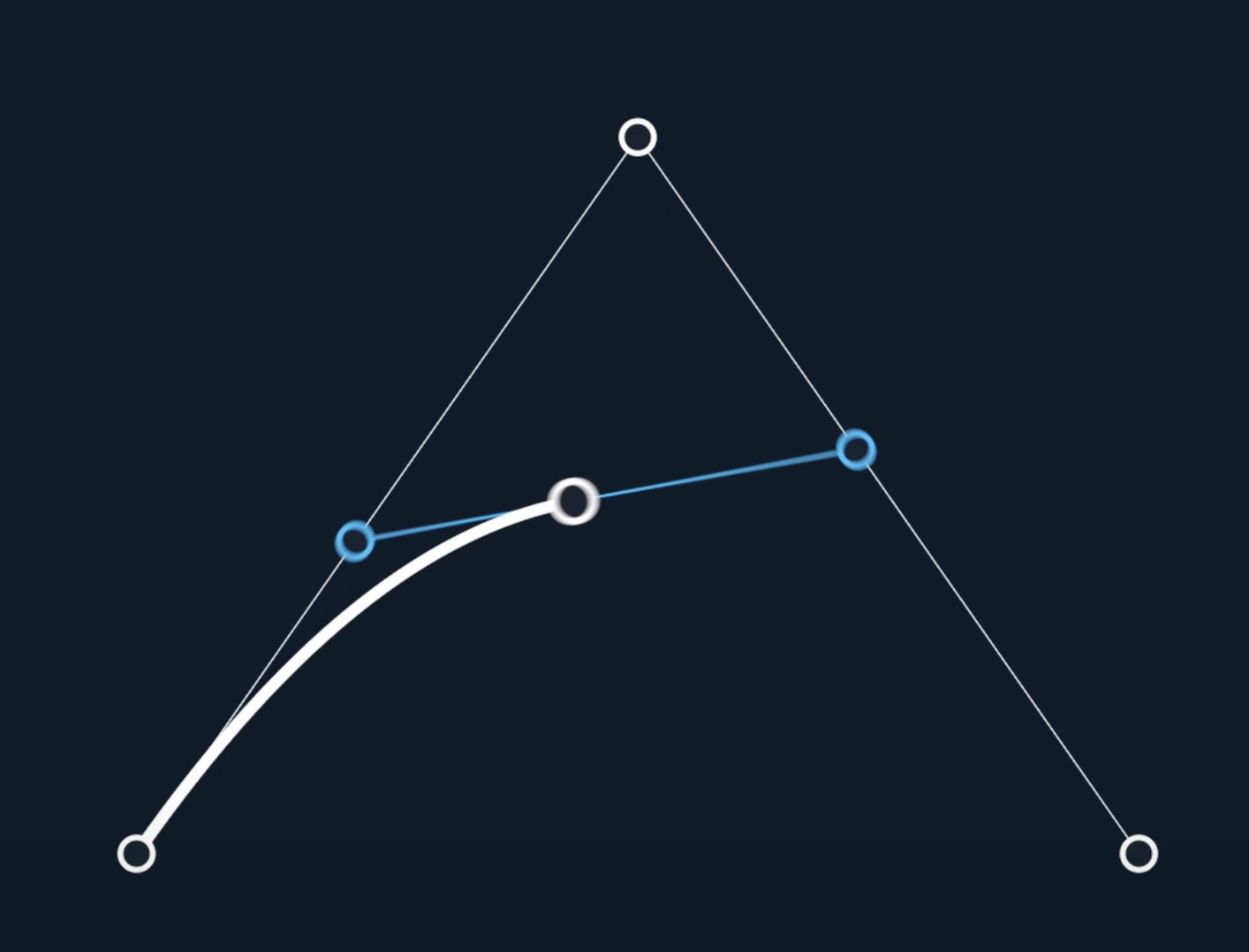
该曲线就是二次贝塞尔曲线

Three Times Bézier curves

如果我们继续添加一个点会发生什么

我们重复同样的过程增加每一条线段的插值点

最后一个插值点将会描述三次贝塞尔曲线的路径

这种结构的美妙之处在于无论使用什么轨迹都有效, 所以我们可以改变线段的轨迹，并且遵循相同的规则，总能给我们一条平滑的曲线

我们主要关注三次贝塞尔曲线这个是最常用的曲线

展开所有多项式方法之后

function lerp (P0, P1, T) {
  return (1 - T)P0 + TP1
}

A = lerp(P0, P1, t)
B = lerp(P1, P2, t)
C = lerp(P2, P3, t)
D = lerp(A, B, t)
E = lerp(B, C, t)
P = lerp(D, E, t)

function lerp (P0, P1, T) {
  return (1 - T)P0 + TP1
}

A = lerp(P0, P1, t)
B = lerp(P1, P2, t)
C = lerp(P2, P3, t)
D = lerp(A, B, t)
E = lerp(B, C, t)
P = lerp(D, E, t)

What is a lerp

学习 lerps 函数 https://zhuanlan.zhihu.com/p/114898567

https://juejin.cn/post/6844903774117429261#comment

贝塞尔曲线（Bezier Curve）是一种广泛应用于计算机图形学和计算机辅助设计的数学曲线，由法国数学家 Pierre Bézier 提出。它通过控制点和插值的方式来绘制曲线，可以用来描述各种各样的形状和路径，例如自然曲线、平滑曲线、锐角曲线等。

贝塞尔曲线由两个或多个控制点组成，其中第一个和最后一个控制点被称为端点，其他控制点则被称为中间点。曲线的形状和路径则由这些控制点的位置和数量决定。在计算机图形学中，我们通常使用二次贝塞尔曲线和三次贝塞尔曲线来绘制曲线。

二次贝塞尔曲线由两个端点和一个控制点组成，可以用如下的数学公式来描述：

bash

B(t) = (1-t)^2 * P0 + 2*t*(1-t) * P1 + t^2 * P2

B(t) = (1-t)^2 * P0 + 2*t*(1-t) * P1 + t^2 * P2

其中，P0、P1 和 P2 分别表示起点、控制点和终点，t 表示曲线的参数，取值范围为 0 到 1，表示曲线上的位置。通过不同的控制点和参数值，我们可以绘制出各种不同的曲线形状。

三次贝塞尔曲线由两个端点和两个控制点组成，可以用如下的数学公式来描述：

bash

B(t) = (1-t)^3 * P0 + 3*t*(1-t)^2 * P1 + 3*t^2*(1-t) * P2 + t^3 * P3

B(t) = (1-t)^3 * P0 + 3*t*(1-t)^2 * P1 + 3*t^2*(1-t) * P2 + t^3 * P3

其中，P0、P1、P2 和 P3 分别表示起点、第一个控制点、第二个控制点和终点，t 表示曲线的参数，取值范围为 0 到 1，表示曲线上的位置。通过不同的控制点和参数值，我们可以绘制出各种不同的曲线形状。

总的来说，贝塞尔曲线是一种灵活、可定制化的曲线绘制方式，可以用来绘制各种各样的形状和路径。在计算机图形学和计算机辅助设计中广泛应用，例如在 Adobe Illustrator、Photoshop 等设计软件中就有贝塞尔曲线工具，可以用来绘制各种复杂的形状。

当我们使用贝塞尔曲线时，我们需要指定曲线的控制点。控制点可以看作是曲线的“吸引点”，它们决定了曲线的弯曲程度和方向。

一条贝塞尔曲线通常由起点、终点和控制点构成。起点和终点分别是曲线的起点和终点，而控制点则是控制曲线的形状。

贝塞尔曲线分为一次、二次、三次和高次曲线。一次曲线由两个点组成，没有控制点，只是一条直线。二次曲线由三个点组成，有一个控制点，曲线是一条弯曲的线。三次曲线由四个点组成，有两个控制点，曲线的弯曲程度比二次曲线更大。

贝塞尔曲线的形状由控制点的位置和数量决定。当控制点靠近起点或终点时，曲线会变得更平直；当控制点远离起点或终点时，曲线会变得更弯曲。同时，如果有多个控制点，它们的位置和相对位置也会影响曲线的形状。

贝塞尔曲线在计算机图形学中广泛应用，可以用于绘制平滑的曲线、动画和变形效果等。

The Beauty of Bézier Curves ​

The Ever so Lovely Bézier Curve ​

What is a Bezier curve? ​

One Times Bézier curves ​

Two Times Bézier curves ​

Three Times Bézier curves ​

What is a lerp ​